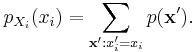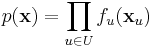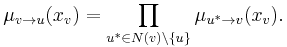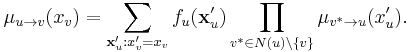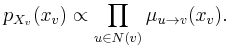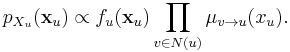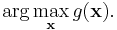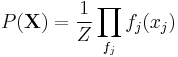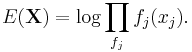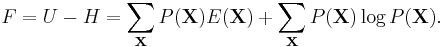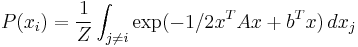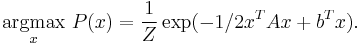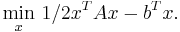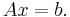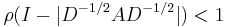Belief propagation

Belief propagation is a message passing algorithm for performing inference on graphical models, such as Bayesian networks and Markov random fields. It calculates the marginal distribution for each unobserved node, conditional on any observed nodes. Belief propagation is commonly used in artificial intelligence and information theory and has demonstrated empirical success in numerous applications including low-density parity-check codes, turbo codes, free energy approximation, and satisfiability[1].

The algorithm was first proposed by Judea Pearl in 1982,[2] who formulated this algorithm on trees, and was later extended to polytrees.[3] It has since been shown to be a useful approximate algorithm on general graphs.[4]

If X=(Xv) is a set of discrete random variables with a joint mass function p, the marginal distribution of a single Xi is simply the summation of p over all other variables:

p_{X_i}(x_i) = \sum_{\mathbf{x}': x'_i=x_i} p(\mathbf{x}').

However this quickly becomes computationally prohibitive: if there are 100 binary variables, then one needs to sum over 299 ≈ 6.338 × 1029 possible values. By exploiting the graphical structure, belief propagation allows the marginals to be computed much more efficiently.

Contents

Description of the sum-product algorithm

Belief propagation operates on a factor graph: a bipartite graph containing nodes corresponding to variables V and factors U, with edges between variables and the factors in which they appear. We can write the joint mass function:

p(\mathbf{x}) = \prod_{u \in U} f_u (\mathbf{x}_u)

where xu is the vector of neighbouring variable nodes to the factor node u. Any Bayesian network or Markov random field can be represented as a factor graph.

The algorithm works by passing real valued functions called messages along the edges between the nodes. These contain the "influence" that one variable exerts on another. There are two types of messages:

\mu_{v \to u} (x_v) = \prod_{u^* \in N(v)\setminus\{u\} } \mu_{u^* \to v} (x_v).
where N(v) is the set of neighbouring (factor) nodes to v. If 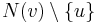N(v)\setminus\{u\} is empty, then 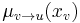\mu_{v \to u}(x_v) is set to the uniform distribution.
\mu_{u \to v} (x_v) = \sum_{\mathbf{x}'_u:x'_v=x_v } f_u (\mathbf{x}'_u) \prod_{v^* \in N(u) \setminus \{v\}} \mu_{v^* \to u} (x'_{u}).
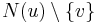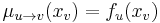where N(u) is the set of neighbouring (variable) nodes to u. If N(u) \setminus \{v\} is empty then \mu_{u \to v} (x_v) = f_u(x_v).

The name of the algorithm is clear from the previous formula: the complete marginalisation is reduced to a sum of products of simpler terms than the ones appearing in the full joint distribution.

Exact algorithm for trees

The simplest form of the algorithm is when the factor graph is a tree: in this case the algorithm computes exact marginals, and terminates after 2 steps.

Before starting, the graph is orientated by designating one node as the root; any non-root node which is connected to only one other node is called a leaf.

In the first step, messages are passed inwards: starting at the leaves, each node passes a message along the (unique) edge towards the root node. The tree structure guarantees that it is possible to obtain messages from all other adjoining nodes before passing the message on. This continues until the root has obtained messages from all of its adjoining nodes.

The second step involves passing the messages back out: starting at the root, messages are passed in the reverse direction. The algorithm is completed when all leaves have received their messages.

Upon completion, the marginal distribution of each node is proportional to the product of all messages from adjoining factors (missing the normalization constant):

p_{X_v} (x_v) \propto \prod_{u \in N(v)} \mu_{u \to v} (x_v).

Likewise, the joint marginal distribution of the set of variables belonging to one factor is proportional to the product of the factor and the messages from the variables:

p_{X_u} (\mathbf{x}_u) \propto f_u(\mathbf{x}_u) \prod_{v \in N(u)} \mu_{v \to u} (x_u).

These can be shown by mathematical induction.

Approximate algorithm for general graphs

Curiously, nearly the same algorithm is used in general graphs. The algorithm is then sometimes called "loopy" belief propagation, because graphs typically contain cycles, or loops. The procedure must be adjusted slightly because graphs might not contain any leaves. Instead, one initializes all variable messages to 1 and uses the same message definitions above, updating all messages at every iteration (although messages coming from known leaves or tree-structured subgraphs may no longer need updating after sufficient iterations). It is easy to show that in a tree, the message definitions of this modified procedure will converge to the set of message definitions given above within a number of iterations equal to the diameter of the tree.

The precise conditions under which loopy belief propagation will converge are still not well understood; it is known that graphs containing a single loop will converge to a correct solution.[5] Several sufficient (but not necessary) conditions for convergence of loopy belief propagation to a unique fixed point exist.[6] There exist graphs which will fail to converge, or which will oscillate between multiple states over repeated iterations. Techniques like EXIT charts can provide an approximate visualisation of the progress of belief propagation and an approximate test for convergence.

There are other approximate methods for marginalization including variational methods and Monte Carlo methods.

One method of exact marginalization in general graphs is called the junction tree algorithm, which is simply belief propagation on a modified graph guaranteed to be a tree. The basic premise is to eliminate cycles by clustering them into single nodes.

Related algorithm and complexity issues

A similar algorithm is commonly referred to as the Viterbi algorithm, but also known as the max-product or min-sum algorithm, which solves the related problem of maximization, or most probable explanation. Instead of attempting to solve the marginal, the goal here is to find the values 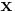\mathbf{x} that maximises the global function (i.e. most probable values in a probabilistic setting), and it can be defined using the arg max:

\arg\max_{\mathbf{x}} g(\mathbf{x}).

An algorithm that solves this problem is nearly identical to belief propagation, with the sums replaced by maxima in the definitions.

It is worth noting that inference problems like marginalization and maximization are NP-hard to solve exactly and approximately (at least for relative error) in a graphical model. More precisely, the marginalization problem defined above is #P-complete and maximization is NP-complete.

Relation to free energy

The sum-product algorithm is related to the calculation of free energy in thermodynamics. Let Z be the partition function. A probability distribution

P(\mathbf{X}) = \frac{1}{Z} \prod_{f_j} f_j(x_j)

(as per the factor graph representation) can be viewed as a measure of the internal energy present in a system, computed as

E(\mathbf{X}) = \log \prod_{f_j} f_j(x_j).

The free energy of the system is then

F = U - H = \sum_{\mathbf{X}} P(\mathbf{X}) E(\mathbf{X}) %2B \sum_{\mathbf{X}} P(\mathbf{X}) \log P(\mathbf{X}).

It can then be shown that the points of convergence of the sum-product algorithm represent the points where the free energy in such a system is minimized. Similarly, it can be shown that a fixed point of the iterative belief propagation algorithm in graphs with cycles is a stationary point of a free energy approximation.

Generalized belief propagation (GBP)

Belief propagation algorithms are normally presented as messages update equations on a factor graph, involving messages between variable nodes and their neighboring factor nodes and vice versa. Considering messages between regions in a graph is one way of generalizing the belief propagation algorithm. There are several ways of defining the set of regions in a graph that can exchange messages. One method uses ideas introduced by Kikuchi in the physics literature, and is known as Kikuchi's cluster variation method.

Improvements in the performance of belief propagation algorithms are also achievable by breaking the replicas symmetry in the distributions of the fields (messages). This generalization leads to a new kind of algorithm called survey propagation (SP), which have proved to be very efficient in NP-complete problems like satisfiability[1] and graph coloring.

The cluster variational method and the survey propagation algorithms are two different improvements to belief propagation. The name generalized survey propagation (GSP) is waiting to be assigned to the algorithm that merges both generalizations.

Gaussian belief propagation (GaBP)

Gaussian belief propagation is a variant of the belief propagation algorithm when the underlying distributions are Gaussian. The first work analyzing this special model was the seminal work of Weiss and Freeman [7]

The GaBP algorithm solves the following marginalization problem:

P(x_i) = \frac{1}{Z} \int_{j \ne i} \exp(-1/2x^TAx %2B b^Tx)\,dx_j

where Z is a normalization constant, A is a symmetric positive definite matrix (inverse covariance matrix a.k.a precision matrix) and b is the shift vector.

Equivalently, it can be shown that using the Gaussian model, the solution of the marginalization problem is equivalent to the MAP assignment problem:

\underset{x}{\operatorname{argmax}}\ P(x) = \frac{1}{Z} \exp(-1/2x^TAx %2B b^Tx).

This problem is also equivalent to the following minimization problem of the quadratic form:

\underset{x}{\operatorname{min}}\ 1/2x^TAx - b^Tx.

Which is also equivalent to the linear system of equations

Ax = b.

Convergence of the GaBP algorithm is easier to analyze (relatively to the general BP case) and there are two known sufficient convergence conditions. The first one was formulated by Weiss et al. in the year 2000, when the information matrix A is diagonally dominant. The second convergence condition was formulated by Johnson et al.[8] in 2006, when the spectral radius of the matrix

\rho (I - |D^{-1/2}AD^{-1/2}|) < 1 \,

where D = diag(A).

The GaBP algorithm was linked to the linear algebra domain,[9] and it was shown that the GaBP algorithm can be viewed as an iterative algorithm for solving the linear system of equations Ax = b where A is the information matrix and b is the shift vector. The known convergence conditions of the GaBP algorithm are identical to the sufficient conditions of the Jacobi method. Empirically, the GaBP algorithm is shown to converge faster than classical iterative methods like the Jacobi method, the Gauss–Seidel method, successive over-relaxation, and others.[10] Additionally, the GaBP algorithm is shown to be immune to numerical problems of the preconditioned Conjugate Gradient method [11]

Recently, a double-loop technique was introduced to force convergence of the GaBP algorithm to the correct solution even when the sufficient conditions for convergence do not hold. The double loop technique works for either positive definite or column dependent matrices.[12]

Notes

  1. ^ a b Braunstein, A.; Mézard, R.; Zecchina, R. (2005). "Survey propagation: An algorithm for satisfiability". Random Structures & Algorithms 27 (2): 201–226. doi:10.1002/rsa.20057. 
  2. ^ Pearl, Judea (1982). "Reverend Bayes on inference engines: A distributed hierarchical approach". Proceedings of the Second National Conference on Artificial Intelligence. AAAI-82: Pittsburgh, PA. Menlo Park, California: AAAI Press. pp. 133–136. https://www.aaai.org/Papers/AAAI/1982/AAAI82-032.pdf. Retrieved 2009-03-28. 
  3. ^ Kim, Jin H.; Pearl, Judea (1983). "A computational model for combined causal and diagnostic reasoning in inference systems". Proceedings of the Eighth International Joint Conference on Artificial Intelligence. 1. IJCAI-83: Karlsruhe, Germany. pp. 190–193. http://dli.iiit.ac.in/ijcai/IJCAI-83-VOL-1/PDF/041.pdf. Retrieved 2009-03-28. 
  4. ^ Pearl, Judea (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference (2nd ed.). San Francisco, CA: Morgan Kaufmann. ISBN 1558604790. 
  5. ^ Weiss, Yair (2000). "Correctness of Local Probability Propagation in Graphical Models with Loops". Neural Computation 12 (1): 1–41. doi:10.1162/089976600300015880. 
  6. ^ Mooij, J; Kappen, H (2007). "Sufficient Conditions for Convergence of the Sum–Product Algorithm". IEEE Transactions on Information Theory 53 (12): 4422–4437. doi:10.1109/TIT.2007.909166. 
  7. ^ Weiss, Yair; Freeman, William T. (October 2001). "Correctness of Belief Propagation in Gaussian Graphical Models of Arbitrary Topology". Neural Computation 13 (10): 2173–2200. doi:10.1162/089976601750541769. PMID 11570995. 
  8. ^ Malioutov, Dmitry M.; Johnson, Jason K.; Willsky, Alan S. (October 2006). "Walk-sums and belief propagation in Gaussian graphical models". Journal of Machine Learning Research 7: 2031–2064. http://jmlr.csail.mit.edu/papers/v7/malioutov06a.html. Retrieved 2009-03-28. 
  9. ^ Gaussian belief propagation solver for systems of linear equations. By O. Shental, D. Bickson, P. H. Siegel, J. K. Wolf, and D. Dolev, IEEE Int. Symp. on Inform. Theory (ISIT), Toronto, Canada, July 2008. http://www.cs.huji.ac.il/labs/danss/p2p/gabp/
  10. ^ Linear Detection via Belief Propagation. Danny Bickson, Danny Dolev, Ori Shental, Paul H. Siegel and Jack K. Wolf. In the 45th Annual Allerton Conference on Communication, Control, and Computing, Allerton House, Illinois, Sept. 07. http://www.cs.huji.ac.il/labs/danss/p2p/gabp/
  11. ^ Distributed large scale network utility maximization. D. Bickson, Y. Tock, A. Zymnis, S. Boyd and D. Dolev. In the International symposium on information theory (ISIT), July 2009. http://www.cs.huji.ac.il/labs/danss/p2p/gabp/
  12. ^ Fixing convergence of Gaussian belief propagation. J. K. Johnson, D. Bickson and D. Dolev. In the International symposium on information theory (ISIT), July 2009. http://www.cs.huji.ac.il/labs/danss/p2p/gabp/

References